My research style

I pursue answers to the simple yet fundamental question of “What is spacetime?” and study quantum theory of spacetime (quantum gravity). At present, the fundamental principles of quantum gravity remain unknown. Therefore, rather than specializing in a specific theory (such as string theory), I explore the principles of quantum gravity from a broad intersection of the three fundamental laws of physics: quantum theory, general relativity, and thermodynamics. What particularly interests me is the relationship between these three laws. For example, if spacetime is a collection of “spacetime atoms” that behave quantum mechanically, it would be a kind of quantum many-body system, and its macroscopic behavior would be determined by statistical and thermodynamic behavior. In this way, at/near the Planck scale, quantum theory, gravity, and thermodynamics should interact and intertwine, potentially giving rise to new laws and behaviors. I am interested in a wide range of theoretical physics and collaborate with researchers around the world to study quantum gravity through the fusion of the principles. For example, my research includes the following.

Research 1: Quantum Black Holes

The true identity of the “objects” we recognize as “black holes” is still unknown. Classically, they are defined as spacetime regions of strong gravity with a horizon. However, current observational results (such as gravitational waves and imaging) originate from the surroundings of the object, and the existence of the horizon has not been confirmed yet. Additionally, three theoretical problems exist: the formation of singularities, the microscopic origin of the entropy-area law, and the information loss problem. While most existing approaches are specialized for each problem, nature should only allow a description that simultaneously resolves all the three.

I have set aside the classical description and reconsidered black holes from the beginning as quantum objects. What, then, is the quantum definition of a black hole? I have proposed two definitions:

Definition 1: “A black hole is the most compact object formed by gravitational collapse following quantum dynamics.”

Definition 2: “A black hole is the configuration that maximizes entropy for a given surface area.”

As a first step in investigating Definition 1, I analyzed the time evolution of spherically symmetric collapsing matter using the semi-classical Einstein equations (a low-energy effective theory of quantum gravity that treats gravity classically and matter quantum mechanically in a mean-field approximation). This analysis revealed that no horizon forms, and instead a high-density object emerges (papers [ 2, 4, 5, 7, 11, 15]). This is a configuration where numerous excited quanta gather due to self-gravity (gravity condensate) and is described by a non-perturbative solution for the Planck constant. As a result, quantum pressure arises due to vacuum fluctuations, supporting the object against self-gravity and resolving the classical singularity. Evaluating the entropy of the matter quanta distributed inside, including self-gravitational effects, exactly reproduces the entropy area law (papers [ 16]). Furthermore, the gravity condensate yields imaging nearly identical to that of classical black holes, and characteristic small deviations are also predicted (paper [ 17]). Interestingly, an investigation of Definition 2 shows that the configuration with maximum entropy agrees with the gravity condensate, leading to the Bousso bound (paper [ 19]). Thus, the gravity condensate, which satisfies both Definitions 1 and 2, is a candidate for quantum black holes.

Currently, we are developing this model and studying the description of black holes as quantum many-body systems beyond the semi-classical approximation.

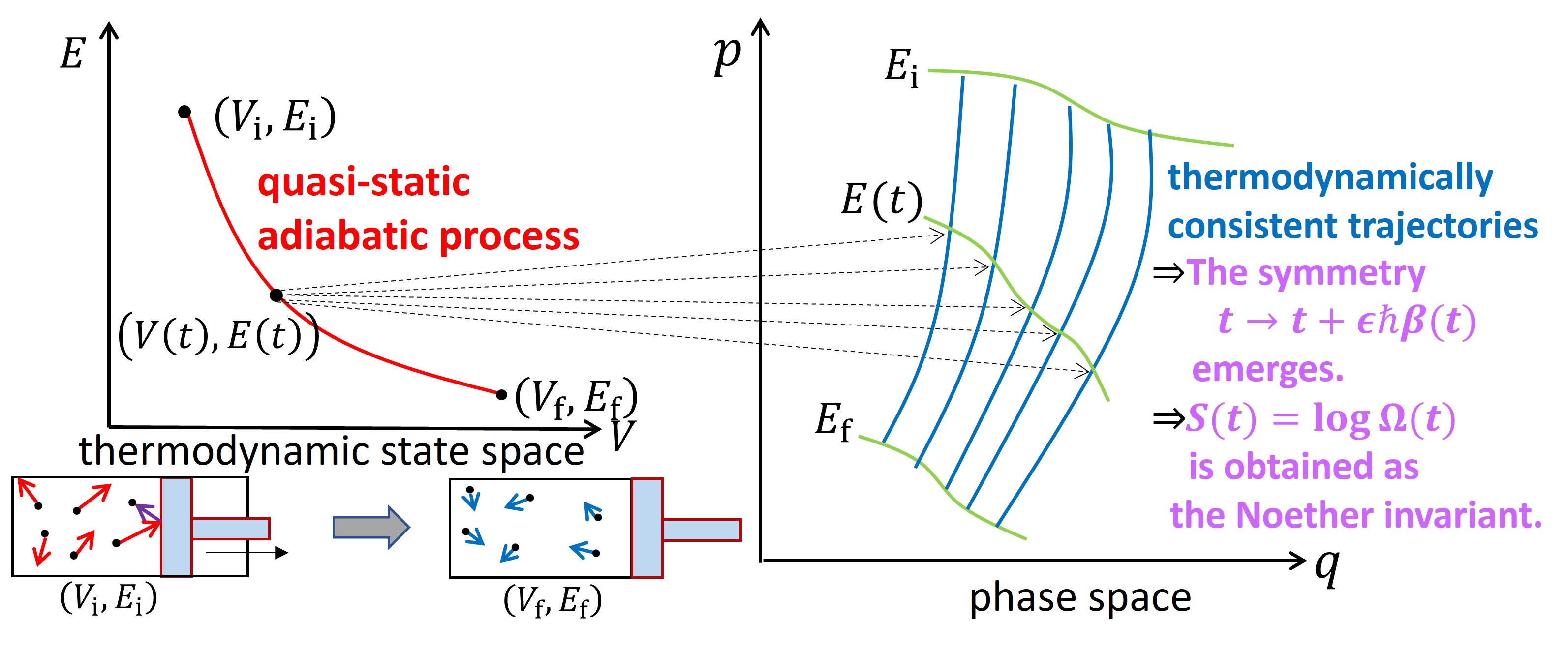
Research 2: Symmetry of thermodynamic entropy

I am also working on fundamental research linking thermodynamics and quantum theory. Thermodynamic entropy is a dynamical quantity that is conserved in adiabatic quasi-static processes (adiabatic invariance, adiabatic theorem). Noether's theorem links conserved quantities and symmetries. So, I wondered, “What symmetry corresponds to the adiabatic invariance of entropy?”

By considering a classical many-body system with a slowly varying external parameter and restricting the domain of the action to a class of trajectories consistent with thermodynamic quasi-static processes, a special time transformation emerges as a symmetry, and the Boltzmann entropy is derived as the Noether invariant (paper[ 6]). Furthermore, constructing the thermodynamic effective wave function of a quantum many-body system as a path integral in the thermodynamic state space, the same symmetry emerges at the quantum level (paper [9]). Thus, this symmetry provides a new characterization of entropy. Interestingly, this symmetry is identical to the symmetry associated with black-hole entropy (Wald entropy). Therefore, it may provide a unified description of gravitational entropy and matter entropy, and serve as a foundation for investigating the statistical behavior of “spacetime atoms.”

Currently, in the framework of the covariant phase space formalism, I am investigating “spacetime entropy” as an adiabatic invariant of gravitational systems by combining this symmetry with the uniqueness theorem of thermodynamic entropy (Lieb-Yngvason).